ARMI: LA TRAIETTORIA E LA RESISTENZA DELL'ARIA
Estratto suntivo dalle pagine del libro di E.Mori e L.Golino "BALISTICA PRATICA" edito da "OLIMPIA"

Una delle trattazioni più difficili nella balistica esterna riguarda la traiettoria di un proiettile nell'atmosfera, infatti quando il moto del proiettile invece che nel vuoto avviene nell'aria, la forza ritardatrice dovuta alla resistenza della stessa è fondamentale per il calcolo della traiettoria e non solo, la viscosità dell'aria varia al variare della sua temperatura e della sua umidità e lungo l'intero spazio percorso dal proiettile in volo, questa temperatura e l'umidità stessa dell'aria può variare in modo repentino e difficile da misurare, per cui ogni calcolo delle traiettorie è puramente teorico se pur molto spesso, se fatto con attenzione, si avvicina di molto a quella che è la vera traiettoria del proiettile.
L'ARIA: un proiettile 9mm (di una munizione 9x19 ad es.) con V0= 330 m/sec, che nel vuoto secondo la formula che vedremo avrebbe una gittata massima di 11.100 mt, nell'aria ha una gittata massima di circa 1.500 metri. Un proiettile da fucile con V0 = 700 m/sec a causa della resistenza dell'aria, subisce una forza ritardatrice che è circa 40 volte maggiore di quella di gravità e la velocità finale, che nel vuoto sarebbe uguale a quella iniziale, viene ridotta a circa 1/6.
Quanto scritto sopra da un idea della complessità dei calcoli da fare per poter disegnare una traiettoria completa e non siamo nemmeno all'inizio. La resistenza che il mezzo (aria o acqua), offre al moto del corpo, è proporzionale alla massa d'aria spostata nell'unità di tempo e viene rappresentata dalla formula fondamentale di Newton
-A- è l'area in mq della sezione normale al movimento del corpo,
-V- è la velocità in mt./sec. (relativa al fluido in cui il corpo è immerso)
-m- è un coefficiente sperimentale che dipende dalla densità del mezzo, aria ( data dalla sua temperatura o altitudine e umidità ), dalla forma e dalla superficie del proiettile. A titolo di curiosità si riportano i valori di -m- determinati all'inizio del secolo da Eiffel mediante sperimentazioni compiute dall'omonima torre:
Superficie piana perpendicolare al moto 0,07
Corpo cilindrico, lunghezza = 1x raggio 0,071
Corpo cilindrico, lunghezza = 2x raggio 0,069
Corpo cilindrico, lunghezza = 3x raggio 0,051
Cono di 60°, punta in avanti 0,015
Emisfero convesso 0,017
Emisfero concavo 0,084
Questi i valori riferiti all'aria, vanno moltiplicati per 800 (circa) se riferiti all'acqua, infatti 800 è il rapporto medio fra la densità dell'acqua e dell'aria alla temperatura ordinaria.
CALCOLI: la formula indicata è puramente orientativa e valida per velocità medie; nel caso di velocità basse, la resistenza varia con tasso inferiore al quadrato della velocità, mentre per velocità elevate la resistenza varia con tasso assai superiore. Il calcolo della resistenza sui proiettili è reso poi ancor più complicato dal fatto che il proietto nel suo volo è soggetto a movimenti oscillanti e di precessione che modificano in ogni istante la sezione opposta al fluido. Per ottenere valori precisi si dovrebbe quindi ricorrere alla ricerca sperimentale della legge di resistenza di ogni singolo proiettile. Per calcoli di una certa approssimazione, si sono però studiate delle leggi generali di resistenza dell'aria, più che sufficienti per gli scopi pratici: dopo aver tracciato sperimentalmente le curve della resistenza dell'aria riferite a diversi tipi di proiettile, si è ricavata una curva riferita ad un "proiettile tipo"; da questa, con l'introduzione di un coefficiente che deriva dal rapporto tra la forma del proiettile rispetto alla forma del proiettile tipo, si può risalire con sufficiente approssimazione ai valori reali. Una delle formule più usate e che, nonostante sia stata elaborata nel 1800 dal balistico russo Majevski, è ancora oggi utilizzata;
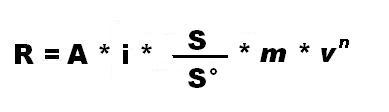
in cui:"R" è la resistenza impressa al proiettile espressa in kg."A" è la sezione del proiettile in mq."i" è un fattore dovuto alla forma che varia, come vedremo, da 0,45 a 2,30 "v" è la velocità del proietto in m/sec. "m" ed "n" sono coefficienti che variano con la velocità e vengono elencati nella seguente tabella:

Infine S/S° sta ad indicare il rapporto fra la densità dell'aria attraversata dal proiettile e la densità "base" pari a kg.1,225 per mq.
PRATICA: ponendo in via generale:
in cui f(v) sta ad indicare la funzione della resistenza in relazione alla velocità, secondo la legge di Majevski o altre analoghe, e ricordando che:
(dove "C" è il calibro in mt.) si ottiene la formula di pratica applicazione
La prima parte del polinomio di destra rappresenta il cosiddetto "coefficiente balistico" (Cb) del proiettile e la formula può essere riscritta cosi:
o ancor meglio cosi:
Una volta nota la resistenza opposta dall'aria, si potrà calcolare la ritardazione (cioè la forza negativa) subita dal proiettile in base alla formula:
e dato che:
si avrà:
Le ultime formule possono naturalmente fondersi assieme ottenendo:
in cui P è espresso in chilogrammi.
IL COEFFICIENTE DI FORMA
In tempi più recenti, in luogo del concetto di coefficiente balistico si è introdotto il concetto di "coefficiente aereodinamico" (o coefficiente di resistenza) "Cw", quantità adimensionale che esprime il comportamento del proiettile dell'aria, variabile anch'essa a seconda dei fattori già ricordati, in funzione della velocità, indicata non in m/sec., ma in rapporto alla velocità del suono, cioè in Mach (velocità del suono = 330 mt/sec = 1 Mach). Cw non è costante in quanto dipende anche dalla viscosità dell'aria e quindi varia continuamente nel corso della traiettoria rendendo i calcoli sensibilmente più dificili. Per ogni proiettile, Cw è infatti funzione di due fattori adimensionali:
1 - il numero di Mach, cioè il rapporto tra velocità del proiettile e velocità del suono;
2 - il numero di Reynolds, cioè il rapporto tra velocità del proiettile e la "viscosità cinematica" dell'aria, moltiplicato per una grandezza che dipende dalla lunghezza del proiettile.
Come si può capire le cose si stanno complicando che probabilmente qualcuno ha già perso il filo del calcolo, chiaramente, il calcolo esatto del Cw è estremamente complesso. Usando il coefficiente Cw, che per i proiettili varia da 0,1 a 0,5 si avrà:
in cui A è la sezione del proiettile in cmq ; S la densità dell'aria in Kg/m3 ; v la velocità del proiettile in "Mach". Premesse le formule matematiche essenziali, vediamo ora di chiarire meglio i valori che sono stati usati e, in primo luogo, f(v), di cui già abbiamo dato l'esempio del Majevski.
STORIA: gli studi per stabilire una legge generale di resistenza dei proiettili (vale a dire in quale modo la resistenza varia con il variare della velocità), sono alquanto datati. Tra il 1872 ed il 1895 nasce la legge di Majevski-Sabuski, nel 1874 quella di Chapel, nel 1888 quella della commissione Gàvre, nel 1894 quella di Vallier, nel 1896 quella dell'italiano Siacci. Ad esse seguiranno quella di Schève (1907), quella di Eberhard-Krupp (1912), di Dupuis-Garnier (1929) e quella sovietica del 1930. Una delle leggi empiriche più usate è quella del Siacci che costituiva il tentativo di unificare il risultato degli esperimenti condotti fino ad allora. Dagli studi si dedusse che la resistenza segue la legge quadratica, vale a dire che la curva di resistenza ha un decorso orizzontale per velocità inferiori alla velocità del suono; attorno alla velocità del suono la resistenza cresce improvvisamente e rapidamente in modo quasi verticale in modo di gran lunga superiore al quadrato della velocità; a velocità superiori a quella del suono la resistenza decresce anche in proporzione inferiore al quadrato della velocità.
Si capisce qui la difficoltà e il perchè non è mai stato prodotto nulla, nel tempo dei computer, capace di dare un esatto risultato per una traiettoria balistica ma semplicemente dei teorici risultati spesso discordanti da quelli pratici.
NUOVI CALCOLI:
la formula per la resistenza, usando i valori K(v) diventa:
Dati i valori di f(v), i valori di K(v) si otterranno con la formula:
Per comodità i valori ottenuti si moltiplicano per 10 al fine di eliminare troppi decimali. Per passare dai valori di K(v).10" , varianti da 1,2 a 7, ai corrispondenti valori di f(v) si userà la formula:
i calcoli elaborati dal Siacci e dagli altri di quel tempo rappresentavano i proiettili di artiglieria del tempo, pesanti e scarsamente aereodinamici. Gli studi successivi adeguarono la curva ai proiettili di artiglieria e di arma leggera più moderni. Questo progresso è stato possibile da quando Prandtl ha studiato il comportamento dei proiettili in apposite gallerie a vento. Da tali studi è emerso che il fluido tende ad unirsi alle pareti del proiettile creando uno "strato limite" le cui linee di corrente che si comportano come un "gas perfetto", questo naturalmente a bassi numeri di Reynolds. Ad elevati numeri di Reynolds, però, si creano turbolenze, tanto sui fianchi, quanto e soprattutto nella parte terminale dei proiettili. Alla base del proiettile si crea un vortice d'aria frenante definito "risucchio" o "vortice di Karman" (in verità questo si forma dietro tutti gli oggetti viaggianti in un fluido). Quest'ultimo fenomeno non è ancora stato studiato con sufficiente esattezza, ma soltanto con formule approssimate. Lo svilupparsi delle turbolenze sui fianchi del proiettile determina l'impennata della curva del Cw in corrispondenza del "muro del suono" a 330 mt/sec. Il risucchio si può ridurre rastremando la base del proiettile; le dimensioni ottimali sono date da una base conica lunga mezzo calibro. La parte appuntita di un proiettile supersonico di profilo ottimale è lunga da 3 a 4 calibri; il proiettile supersonico è lungo da 4,5 a 6 calibri. Gli studi dell'Eberhard hanno condotto alla formulazione della curva di resistenza portante il suo nome, corrispondente alla curva del proiettile tipo Krupp con calibro di 10 cm. e che non si discosta molto da quella del Siacci, ma di uso comune per il fatto che i valori di f(v) sono stati tabellati dal Sangewald per velocità fino a 750 m/s. Tra le varie leggi di resistenza conserva ancora un certo interesse quella già citata del Majevski per il motivo che essa è alla base delle tavole di ritardazione dell' Ingall, ancora utilizzate in America.
Come già detto, la balistica moderna tende ad esprimere la legge di resistenza, non in relazione al coefficiente balistico, ma al coefficiente di resistenza aereodinamica del proiettile, con notevoli vantaggi matematici.
Il coefficiente di forma II
Già abbiamo detto che ogni proiettile ha un suo caratteristico comportamento e che la resistenza dell'aria andrebbe calcolata in ogni caso sperimentalmente per tutto l'arco di velocità possibili. La resistenza dell'aria, oltre che da fattori esterni al proiettile, quali i movimenti oscillatori durante il suo volo è determinata dalla forma della punta del proiettile, dalla lunghezza del suo corpo, dalla forma della coda, dal materiale. L'influenza di questi singoli fattori varia con il variare della velocità. La forma della punta determina il valore dell'onda di pressione frontale esercitata dal fluido sul proiettile; il corpo ed il materiale di rivestimento del proiettile determinano la resistenza di attrito nell'aria; la coda influisce sui valori di risucchio. Se il proiettile ha velocità subsonica, le onde di pressione influiscono poco sulla resistenza, così che essa risulta composta principalmente dall'attrito e dal risucchio. Con l'aumentare della velocità a valori ultrasonici, aumenta anche la componente del fronte di pressione fino a raggiungere circa la metà del valore della resistenza totale. Si comprende quindi la difficoltà di adottare un coefficiente "i" che consenta un perfetto adattamento della curva della legge di resistenza alla curva reale del singolo proiettile. Si ricordi quindi che per il calcolo della resistenza ad una determinata velocità è possibile individuare un coefficiente abbastanza esatto. Invece, per calcoli che comportino lo studio di un'intera traiettoria, ove la velocità del proiettile varia da un massimo ad un minimo, ci si dovrà accontentare di valori medi approssimativi.
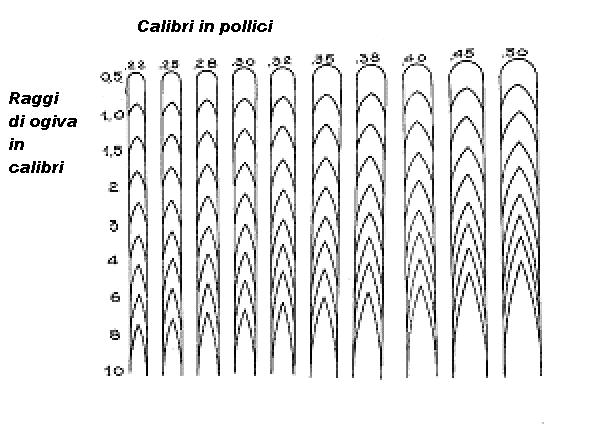
Il coefficiente di forma indica il rapporto tra la resistenza effettiva di un dato proiettile e la resistenza di un proiettile tipo, ciò deriva dal fatto che tale coefficiente non può essere indicato in via generale, ma che esso è sempre ed esclusivamente relativo ad una data legge di resistenza, i coefficienti di forma da impiegare usando i valori del Majevski sono diversi da quelli necessari per i valori del Siacci ed entrambi saranno diversi da quelli da introdurre usando le tavole del Sangewald.
In prima approssimazione si può ritenere che il fattore "i" vari da 0,40 per proiettili militari per moschetto appuntiti, a 1 - 1,2 per proiettili da pistola e rivoltella a punta tondeggiante, fino a 3-4 per proiettili cilindrici (wad cutter). Partendo dalla figura sopra si cerca di individuare, a seconda del calibro indicato, quale sia più o meno il raggio di curvatura dell'ogiva del proiettile e con esso si entra nella figura sotto ove nella prima colonna sono indicati ì valori di "i" per proiettili a punta tondeggiante o appuntita mentre nelle restanti colonne sono indicati valori da sostituire a quelli della prima colonna quando il proiettile è a punta appiattita o cava (a seconda del diametro, espresso in calibri, dell'appiattimento). Per ottenere una ancor maggiore precisione si può tener conto di altri fattori da aggiungere o sottrarre ai valori trovati sopra.
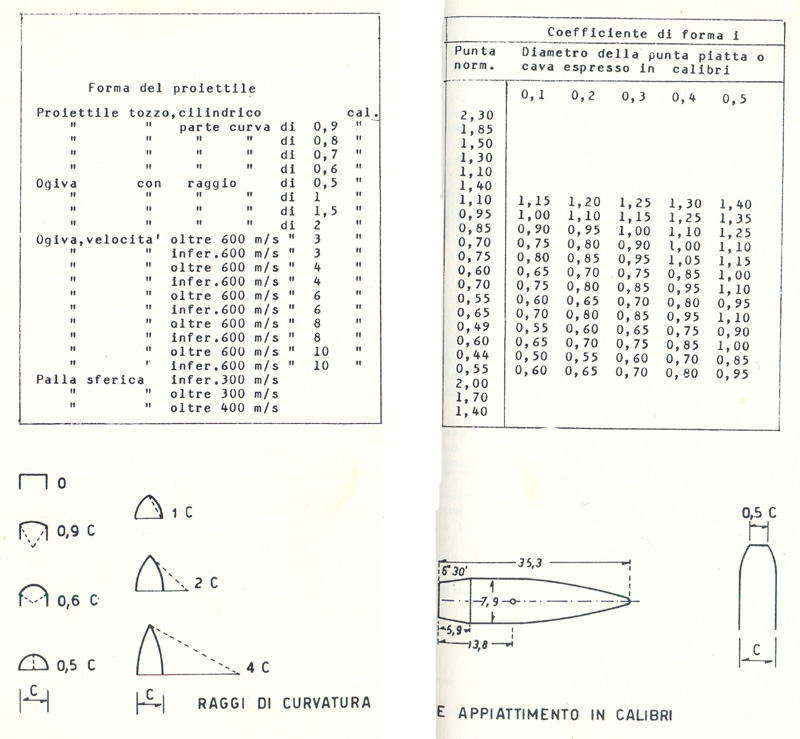
Se il corpo del proiettile (corpo è la parte che viene a contatto con l'anima dell'arma e non comprende perciò l'ogiva e la coda rastremata) è più corto di cinque calibri, il fattore di forma va diminuito delle seguenti quantità:
corpo = 4 calibri -0,01
corpo = 3 calibri -0,03
corpo = 2 calibri -0,04
corpo = 1 calibro -0,05
Il cono di base, con un angolo normale di 15° comporta una diminuzione del coefficiente di forma di -0,08; la presenza di mantellatura sporgente (Scharfrand) comporta un aumento di +0,15; la presenza di punta di piombo fuori mantellatura e lunga più di 0,3 calibri, un aumento di + 0,06. Ad esempio un proiettile 8 x 57 JS HMB Norma a base rastremata e punta di piombo, con ogiva pari a 32 mm e quindi di 4 calibri avrà, in relazione ad una velocità iniziale di 755 m/s
valore base della tabella sopra indicato = 0,60
arrotondamento della punta pari a 0,5 = +0,40
cono di base = -0,08
punta in piombo = +0,06
coefficinete "i" = 1,02
Conoscendo il Cw di un proiettile è possibile risalire con una certa approssimazione al fattore di forma del proiettile stesso in relazione ad una data legge di resistenza e viceversa. Comparando le formule ed eliminando i termini eguali, si ricava infatti
ove' naturalmente la velocità è espressa in Mach e non in m/sec. e quindi
Il coefficiente aereodinamico Cw può essere dedotto dalla differenza di velocità misurate sperimentalmente su di una data distanza, possibilmente breve, secondo la formula
in cui v, e v2 sono le velocità (in m/sec.) iniziali e finali prese in considerazione; "s" è la lunghezza della base di tiro (cioè il tratto di traiettoria) in metri; "F" la sezione in metri quadrati del proiettile; "P" il peso del proiettile in Kg. E' da mettere all'attenzione del lettore che le misurazioni devono essere effettuate con la massima precisione e con prove ripetute in modo da eliminare il più possibile gli errori, poiché piccoli errori nella misurazione comportano errori rilevanti nel risultato.
Eesempio di un proiettile appuntito per K98 (8x57), con V0 = 706 mt/sec e V100 = 660 mt/sec, peso 0,0128 Kg, cal. 0,008 mt.
applicando la formula i = 0, 45 circa.
E' opportuno però far presente che nei calcoli balistici pratici ciò che in genere interessa non è di ottenere gli esatti valori della ritardazione, ma al risultato pratico che gli elementi della traiettoria calcolati corrispondano a quelli effettivi. Perciò avendo a disposizione una tavola di tiro impostata sui valori usuali del coefficiente balistico, dell'angolo di tiro e della gittata e conoscendo per un dato proiettile di cui si ignora la legge di resistenza, quale è la gittata sperimentale per un dato angolo di tiro, si rileva dalla tavola quale è il coefficiente balistico della legge standard corrispondente alla medesima gittata; il rapporto tra il coefficiente così trovato e quello del proiettile in esame indicherà il cosiddetto "coefficiente globale di forma" che consente di rapportare i dati standard della traiettoria, alla traiettoria ricercata. Un procedimento analogo è quello con cui, attraverso le tavole di ritardazione, conosciute le perdite di velocità su di un dato percorso, si risale al coefficiente balistico e da questo al coefficiente di forma "i". Se il percorso è breve si avrà un fattore di forma istantaneo; se il percorso è alquanto lungo, il fattore trovato si può considerare come "globale" dell'intera traiettoria.
In fine ...
LA SCELTA DEL PROIETTILE ADATTO
Ciò che però volevamo farvi capire è che la scelta del proiettile adatto la dove si voglia sfruttare al massimo le proprie capacità di "sniper", quelle dell'arma e quelle della ricarica, non è cosa semplice ne da prendere sotto banco. Per tiri limitati ai classici poligoni che non superano i 100 mt. spesso la differenza tra un proiettile e l'altro non si nota, ma se parliamo di tiro ben oltre i canonici 300 mt. una volta esploso il colpo lasciamo al proiettile tutto il lavoro che abbiamo fatto sperando che sia lui solo a portarlo a termine.
Qqui abbiamo visto che se ci affidiamo a proiettili non adatti o forniamo al nostro proiettile velocità inadeguate, egli vanificherà tutto il lavoro fatto.
Per coloro che male si cimentano con la matematica e la balistica, sapere che la forma, lunghezza e velocità del proiettile contano per un tiro perfetto, sicuramente servirà da oggi a far fare qualche centro in più e speriamo a vincere anche qualche gara .
- data 2024
